古典密码学
代换密码
代换是古典密码中 用到的最基本的处理技巧之一。所谓代换,就是将明文中的一个字母由其它字母、数字或符号替代的一种方法。
凯撒密码
仿射密码

单表代换密码
多表代换密码
维吉尼亚密码

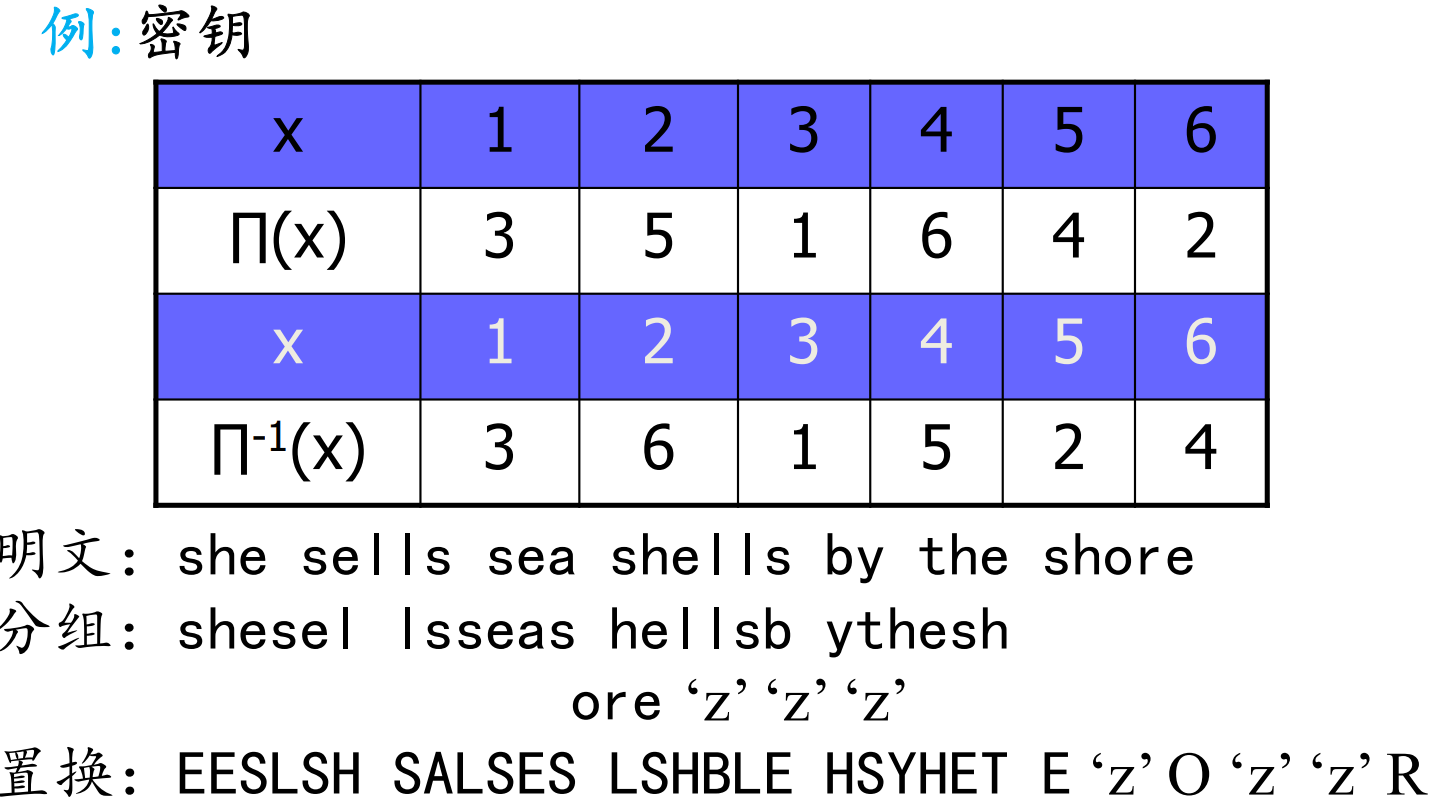
置换密码
是古典密码中用到的 另一个最基本的处理技巧。将明文字符按照某种 规律重新排列而形成密文的过程。
Hill密码
希尔密码

对于密码学中同余矩阵的求法
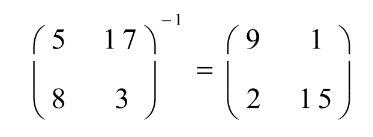
对于二阶矩阵 求其伴随矩阵 (主对调,副变号)
再求其行列式的值与模数的同余的逆元
最后将逆元与伴随矩阵相乘,再对所求矩阵的值进行与模数的同余即可(可以推导)
转轮密码
Enigma密码机
代换密码的唯密文攻击
统计攻击(频率攻击)
'移位密码、仿射密码和单表代换密码'都没 有破坏明文的频率统计规律,可以直接用 统计分析法维吉尼亚密码
第一步:确定密钥长度
方法一:Kasiski测试法
方法二:重合指数法
穷搜密钥字
DES
结构
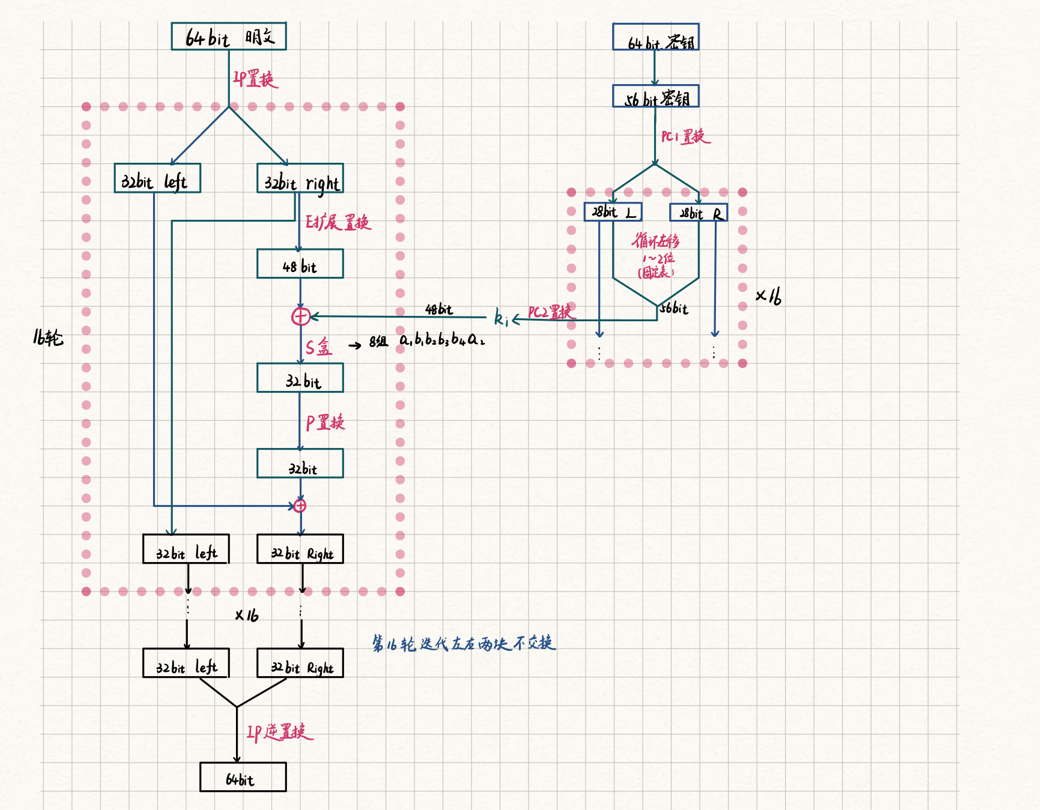
全过程python如下
#密钥编排算法
#pc1置换
def position_change(table, key ,name):
cnt = 0
pc1 =''
print(f'{name} = ',end='')
for i in table:
pc1 += key[i-1]
print(key[i-1],end='')
cnt+=1
if cnt == 4:
print(' ',end='')
cnt = 0
print()
return pc1
#Ci Di
def CiDi_change(i, Ci, Di):
move_int = '1122222212222221'
if(i == 0):
Ci = C0[int(move_int[i]):] + C0[:int(move_int[i])]
Di = D0[int(move_int[i]):] + D0[:int(move_int[i])]
else:
Ci = Ci[int(move_int[i]):] + Ci[:int(move_int[i])]
Di = Di[int(move_int[i]):] + Di[:int(move_int[i])]
return Ci,Di
#E扩展
#密钥加
def key_encrypt(key, text, sorted_num,name):
temp = []
temp_string = ''
cnt = 1
for i in range(len(key)):
temp_string += str(int(key[i]) ^ int(text[i]))
if i%sorted_num == sorted_num-1:
print(f'{name}{cnt} = {temp_string}',end=',')
temp.append(temp_string)
temp_string = ''
cnt += 1
print()
return temp
#S盒
def s_box_change(Bi):
Ci = []
for i in range(8):
print(f'C{i} = ',end='')
row = int(Bi[i][0] + Bi[i][5],2)
line = int(Bi[i][1:5],2)
s_key = str(bin(S_box[i][row][line]))[2:]
if len(s_key) < 4 :
s_key = s_key.rjust(4,'0')
print(s_key,end=',')
Ci.append(s_key)
print()
return Ci
#------------------------------------------------------
while 1:
#ip置换
print('--明文的ip的置换--')
ip_string = position_change(IP,main_string, 'ip_string')
print()
print('--L0R0的生成--')
L0 = ip_string[:int(len(ip_string)/2)]
R0 = ip_string[int(len(ip_string)/2):]
R0 = input('R0 - >')
print(f'L0 = {L0}',end=',')
print(f'R0 = {R0}')
print()
#pc1置换
print('--密钥的pc1置换--')
pc1= position_change(PC_1, key , 'pc1')
C0 = pc1[:int(len(pc1)/2)]
D0 = pc1[int(len(pc1)/2):]
print()
#移位
print('--密钥的CiDi移位--')
i=0
Ci,Di = CiDi_change(i,C0,D0)
i+=1
print(f'Ci = {Ci},Di = {Di}')
print()
#pc2置换
print('--移位后的pc2--')
k1 = position_change(PC_2,Ci + Di,'pc2')
print()
# E扩展
print('--ri的E扩展--')
E_r0 = position_change(E_change,R0,'E_r0')
print()
# 删除E扩展
# E_r0 = R0.ljust(48,'0')
#密钥加
print('--r0与ki的密钥加--')
Bi = key_encrypt(k1, E_r0,6,'B')
print()
#S盒
print('从Bi到Ci的S盒置换,8个S盒,6bit->8bit')
S_Ci = s_box_change(Bi)
print()
# #删除S盒
# S_Ci = []
# for item in Bi:
# S_Ci.append(item[1:5])
#P置换
print('--Ci的P置换--')
S_Ci = ''.join(S_Ci)
f_r0_ki = position_change(P_change,S_Ci,'f(ri-1,ki)')
print()
# # 删除P置换
# S_Ci = ''.join(S_Ci)
# f_r0_ki = S_Ci
#异或--------------------
print('--ri与f(r0,ki)的异或--')
Ri = key_encrypt(L0,f_r0_ki,32,'R')
Ri = ''.join(Ri)
Li = R0
print(f'L1 = {Li}')以下是参数
IP= [58,50,42,34,26,18,10,2,60,52,44,36,28,20,12,4,62,54,46,38,30,22,14,6,64,56,48,40,32,24,16,8,57,49,41,33,25,17,9,1,59,51,43,35,27,19,11,3,61,53,45,37,29,21,13,5,63,55,47,39,31,23,15,7]
E_change = [32,1,2,3,4,5,4,5,6,7,8,9,8,9,10,11,12,13,12,13,14,15,16,17,16,17,18,19,20,21,20,21,22,23,24,25,24,25,26,27,28,29,28,29,30,31,32,1]
PC_1 = [57,49,41,33,25,17,9,1,58,50,42,34,26,18,10,2,59,51,43,35,27,19,11,3,60,52,44,36,63,55,47,39,31,23,15,7,62,54,46,38,30,22,14,6,61,53,45,37,29,21,13,5,28,20,12,4]
PC_2 = [14,17,11,24,1,5,3,28,15,6,21,10,23,19,12,4,26,8,16,7,27,20,13,2,41,52,31,37,47,55,30,40,51,45,33,48,44,49,39,56,34,53,46,42,50,36,29,32]
P_change = [16,7,20,21,29,12,28,17,1,15,23,26,5,18,31,10,2,8,24,14,32,27,3,9,19,13,30,6,22,11,4,25]
key = "1010101100110100100001101001010011011001011100111010001011010011"
main_string = "0011100011010101101110000100001011010101001110011001010111100111"
S_box =[[[14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7],
[0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8],
[4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0],
[15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13]],
[[15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10],
[3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5],
[0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15],
[13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9]],
[[10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8],
[13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1],
[13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7],
[1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12]],
[[7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15],
[12,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9],
[10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4],
[3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14]],
[[2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9],
[14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6],
[4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14],
[11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3]],
[[12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11],
[10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8],
[9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6],
[4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13]],
[[4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1],
[13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6],
[1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2],
[6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12]],
[[13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7],
[1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2],
[7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8],
[2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11]]]AES
加密过程
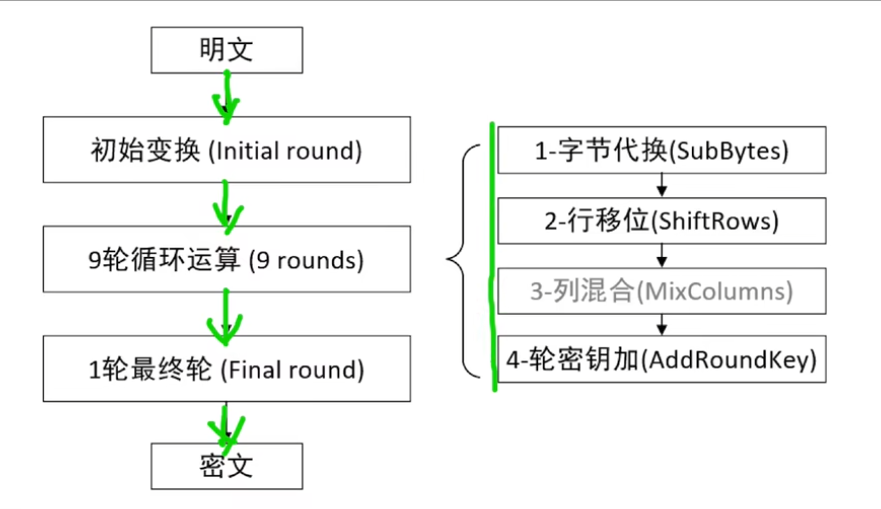
初始变换
1个P代表1个字节 ,所以1个小矩阵就代表 128位
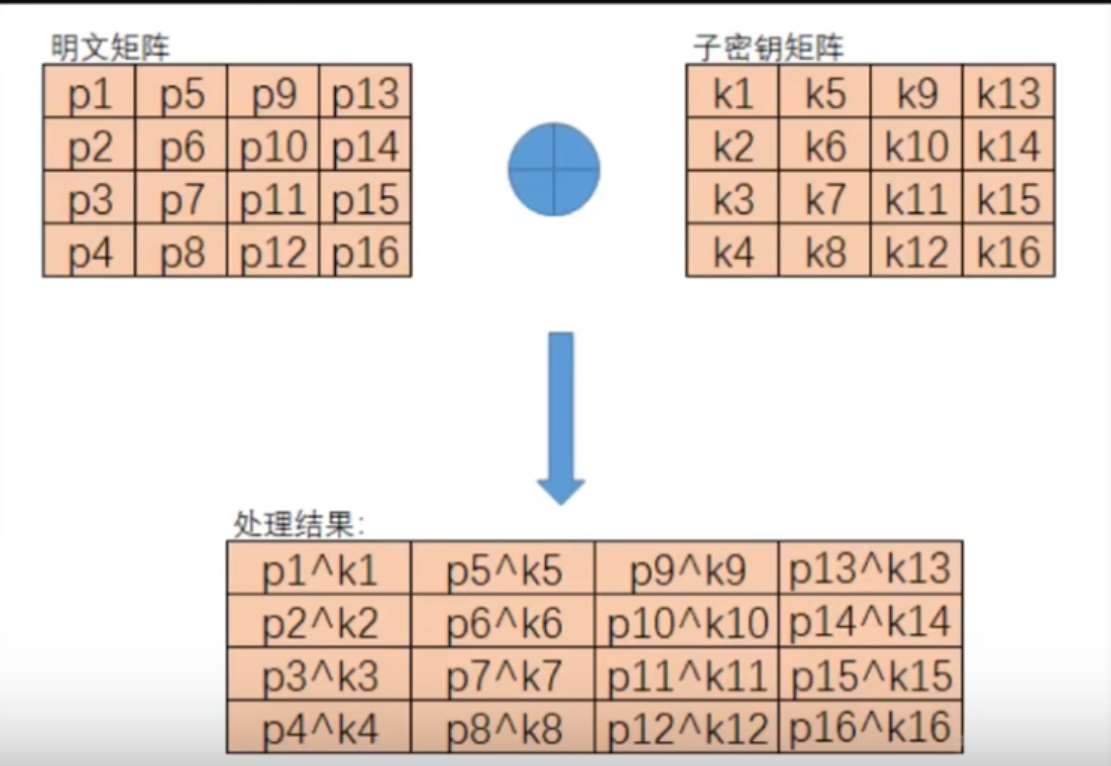
字节代换
4x4 = 0001 1001
19 —> d4 (即第一行第九列,4bit表示行列,1字节有16bit)
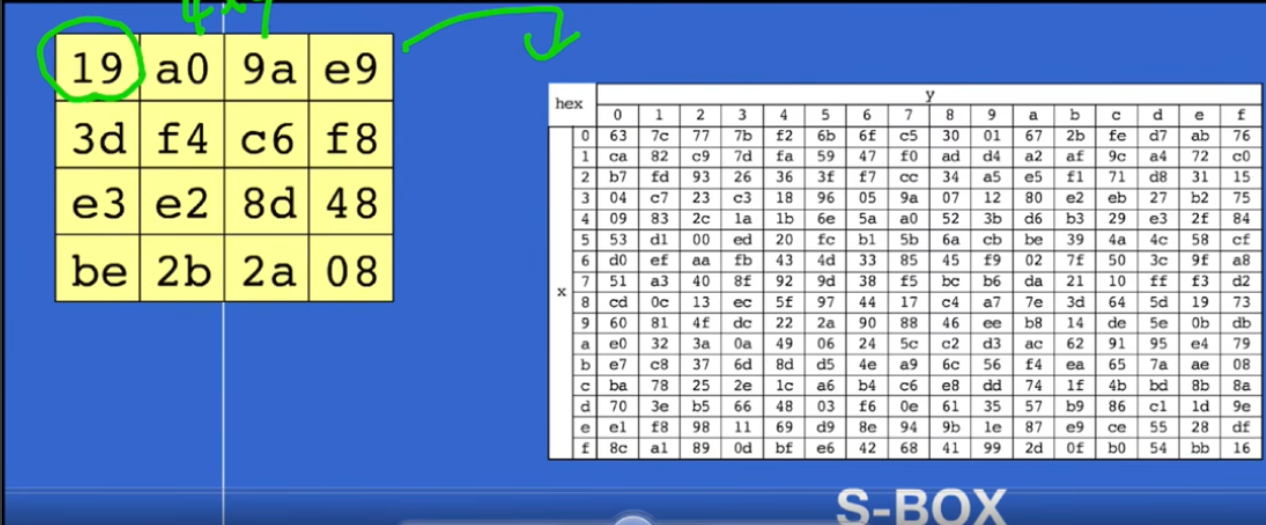
行移位

列混合
将输入的 4*4 矩阵左乘一个给定 4*4矩阵
列混合中,矩阵乘法是在有限域GF(2^8)中 x^8+x^4+x^3+x^1+1
列混合部分
'乘法可以化为多项式计算'
'加法是异或运算。'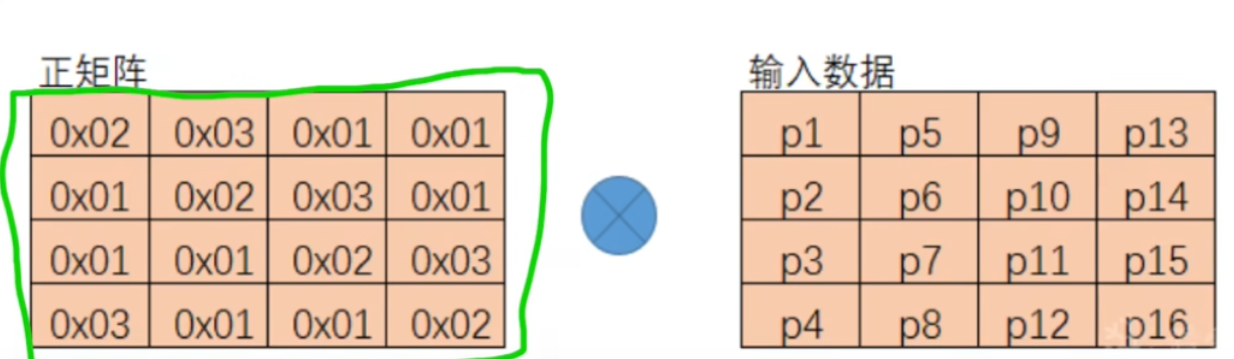
轮密钥加
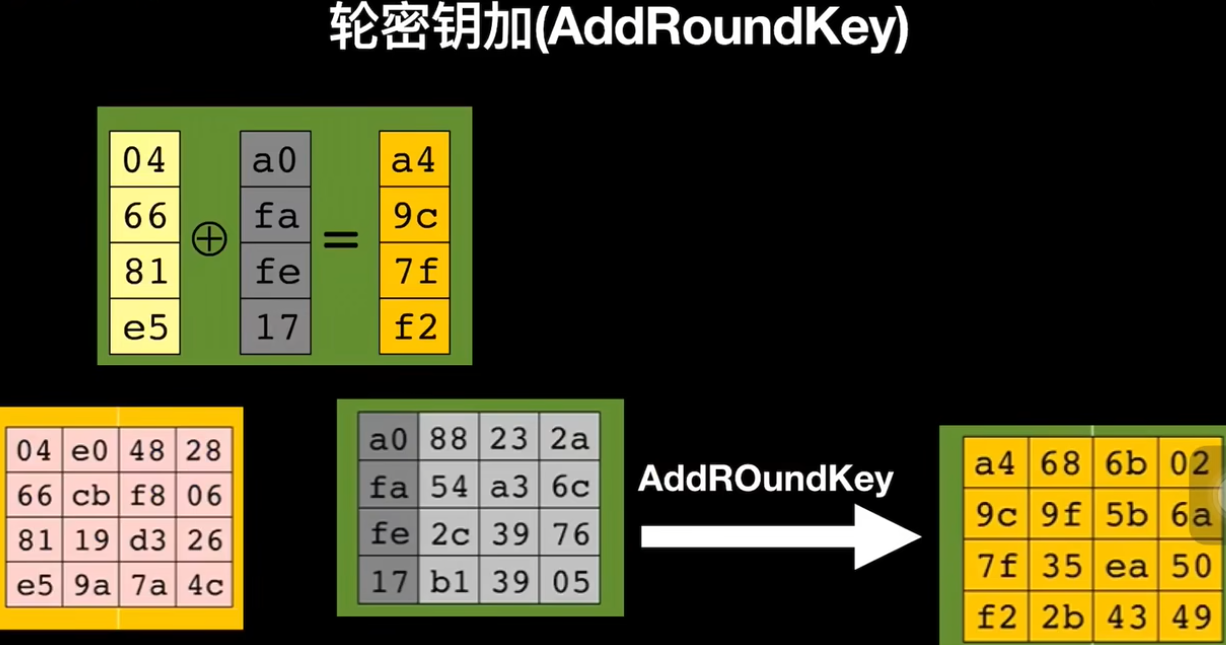
密钥扩展算法

关于T函数
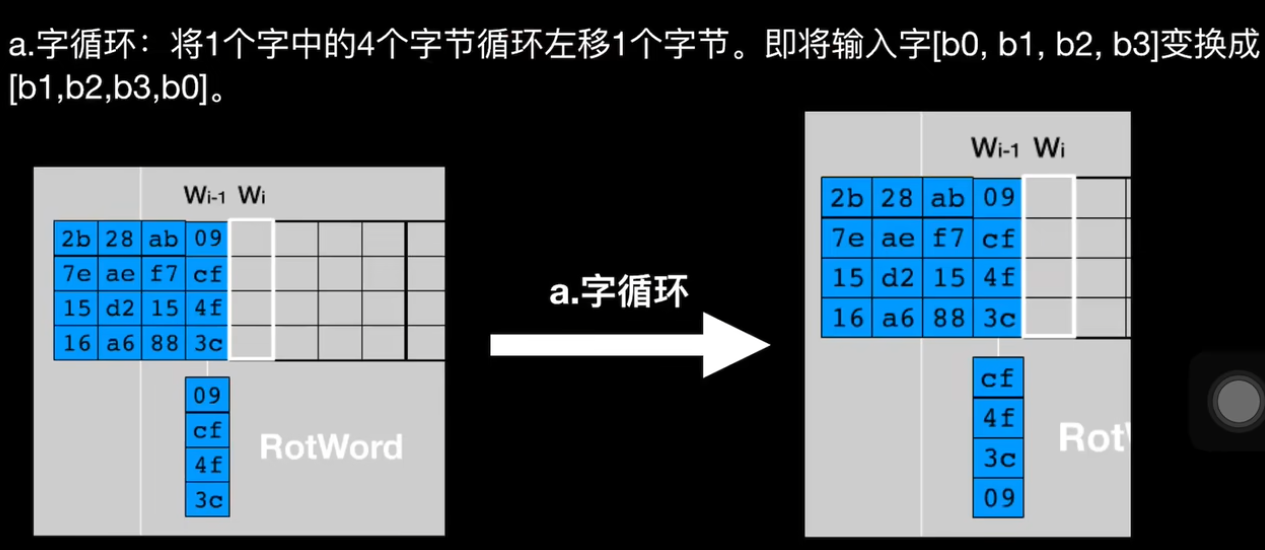
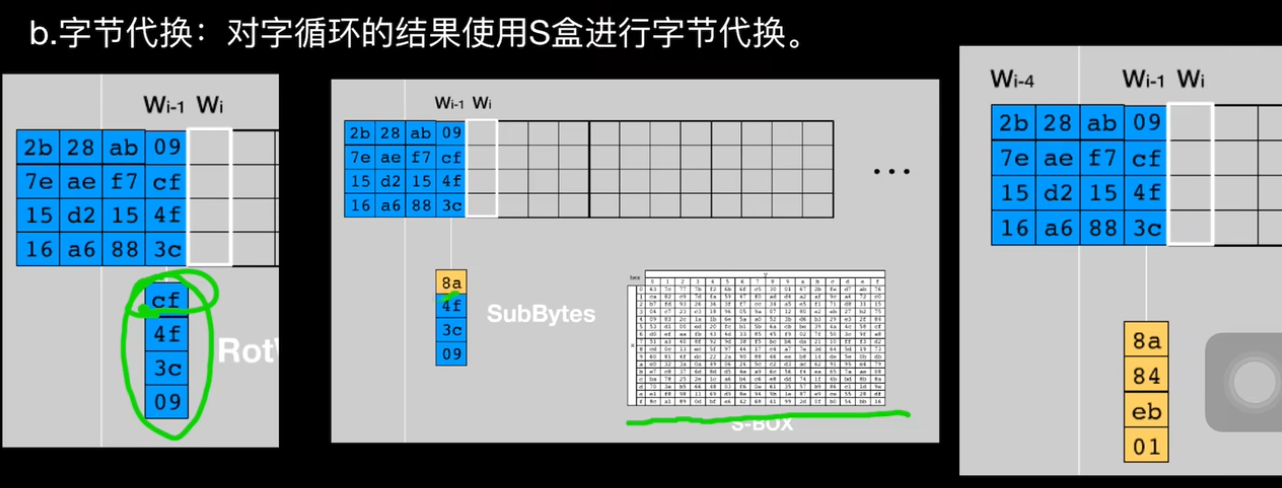
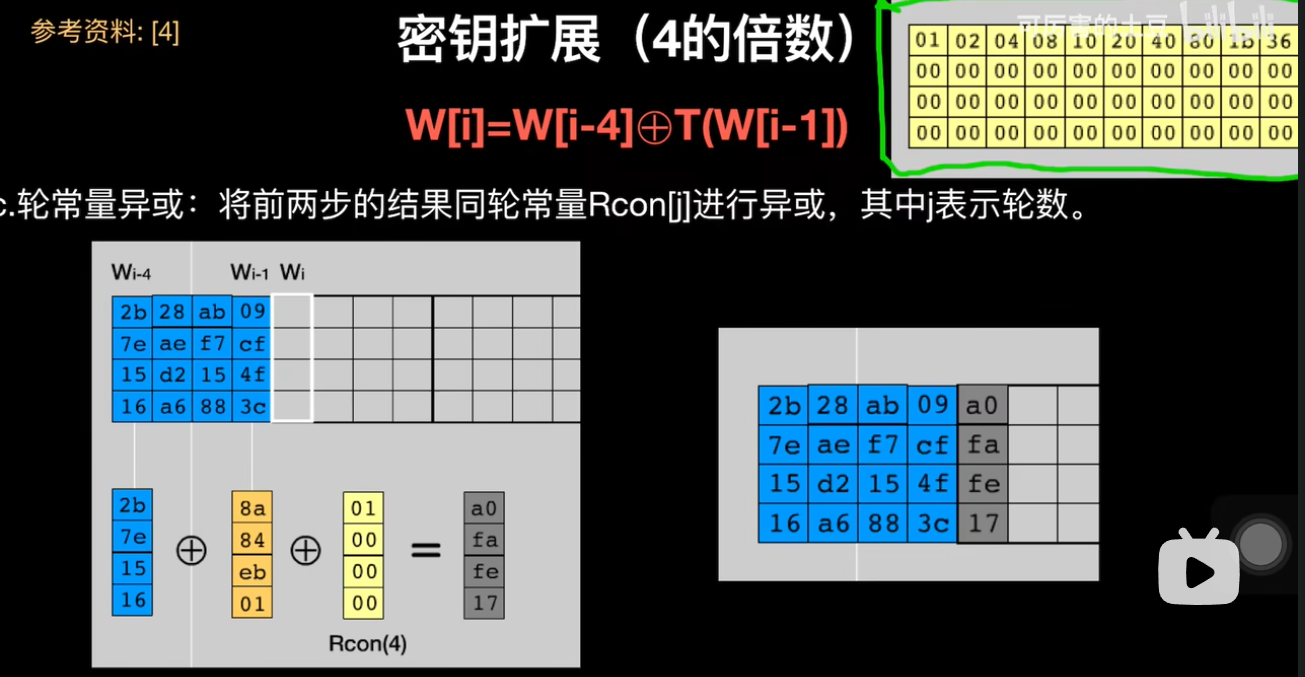
轮常量在右上角是给定的。下面贴一下以上图片出处,来自b站可厉害的土豆分组密码的加密方式
ECB 电码本模式
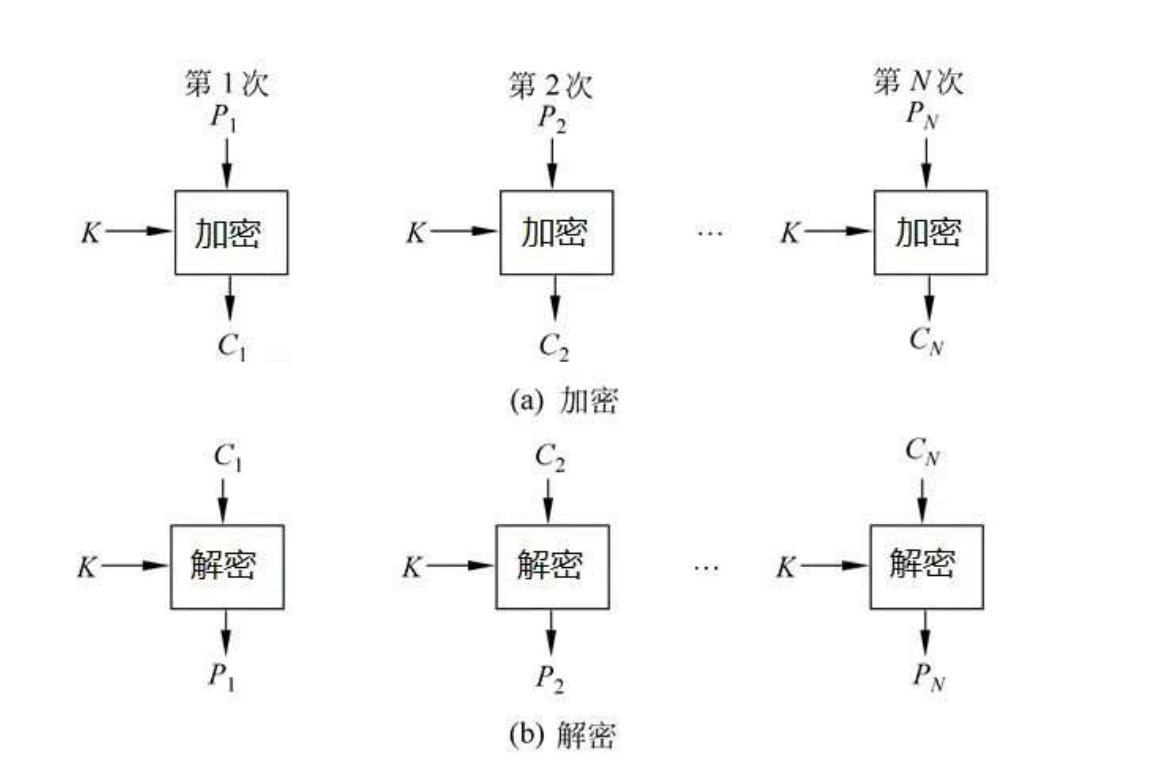
1.适合一个分组长度的短数据加密
2.将长消息分块,若最后一个分块不足分组长度,则需要'填充'
3.加解密不同
4.存在密文扩展
5.密文块分别独立解密,无顺序要求
6.'不存在'错误传播CBC模式 密码分组链接模式
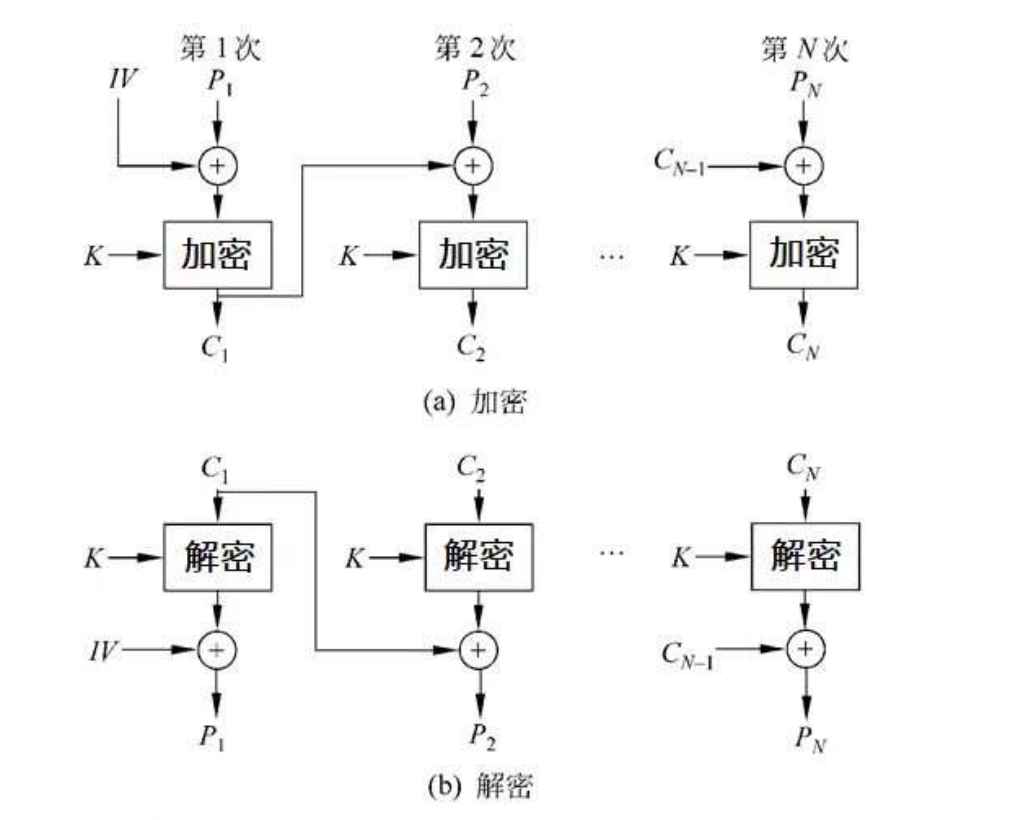
0. '分组密码'
1. 其中IV是每次随机给定的数
2. 适合大于一个分组长度的长数据加密
3. 隐蔽了数据模式
4.加密和解密过程分别调用加密算法和解密算法
5. '解密错误'至多传播两个分组 (看解密前)
6. 加密不能并行,解密可并行处理
7.有'密文扩展'CFB 密码反馈模式
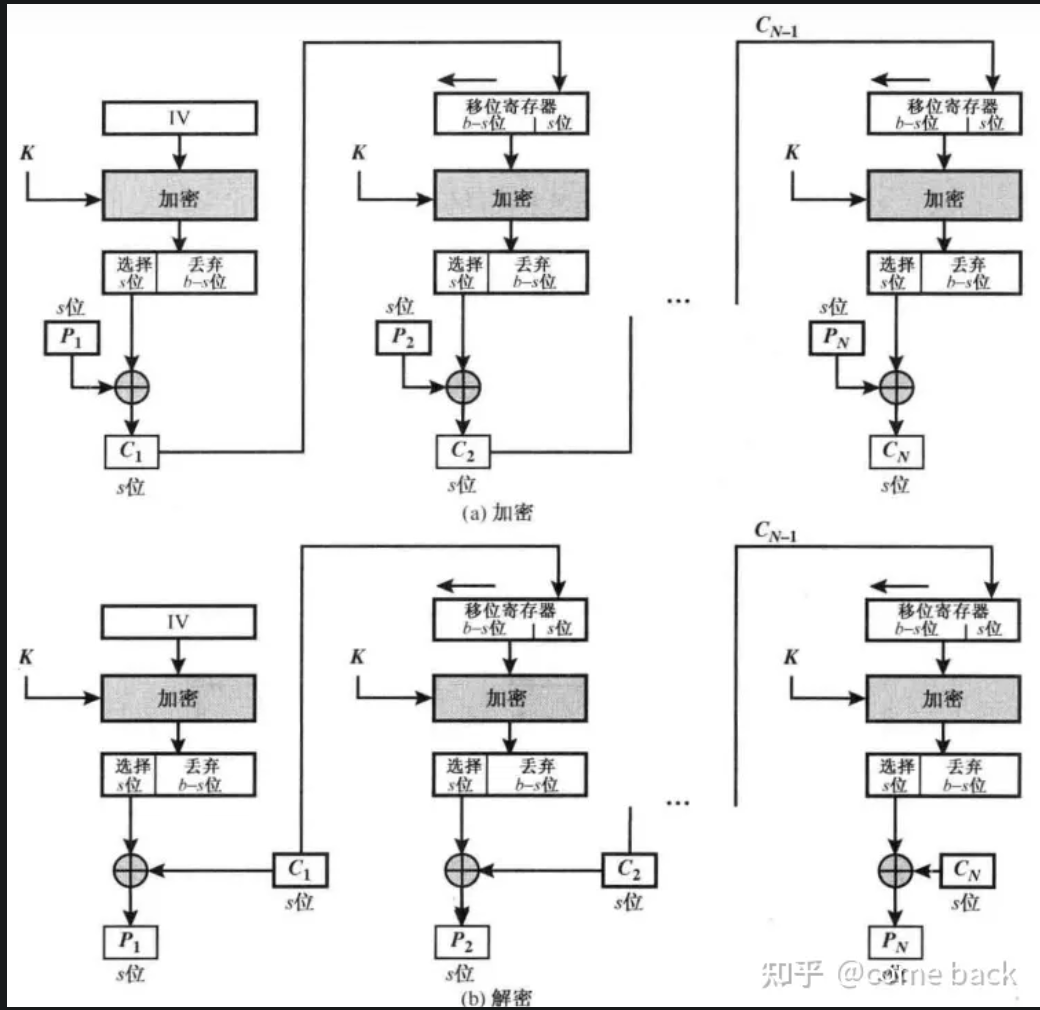
0. '自同步流密码',与前面不同,只是将密钥K进行加密后与明文异或
1.隐蔽了数据模式
2.存在错误传播的可能性:前部分密文出错,会影响后边的解密。这是因为一块密文在进入下一分组的移位寄存器后,会在接下来的几个分组中一直在移位寄存器中。
3.'有自同步功能':在若干分组加密后,前边错误加密的密文会移出移位寄存器,停止对后面分组的加密造成影响。
4. 加密不可并行,解密可并行4.OFB 输出反馈模式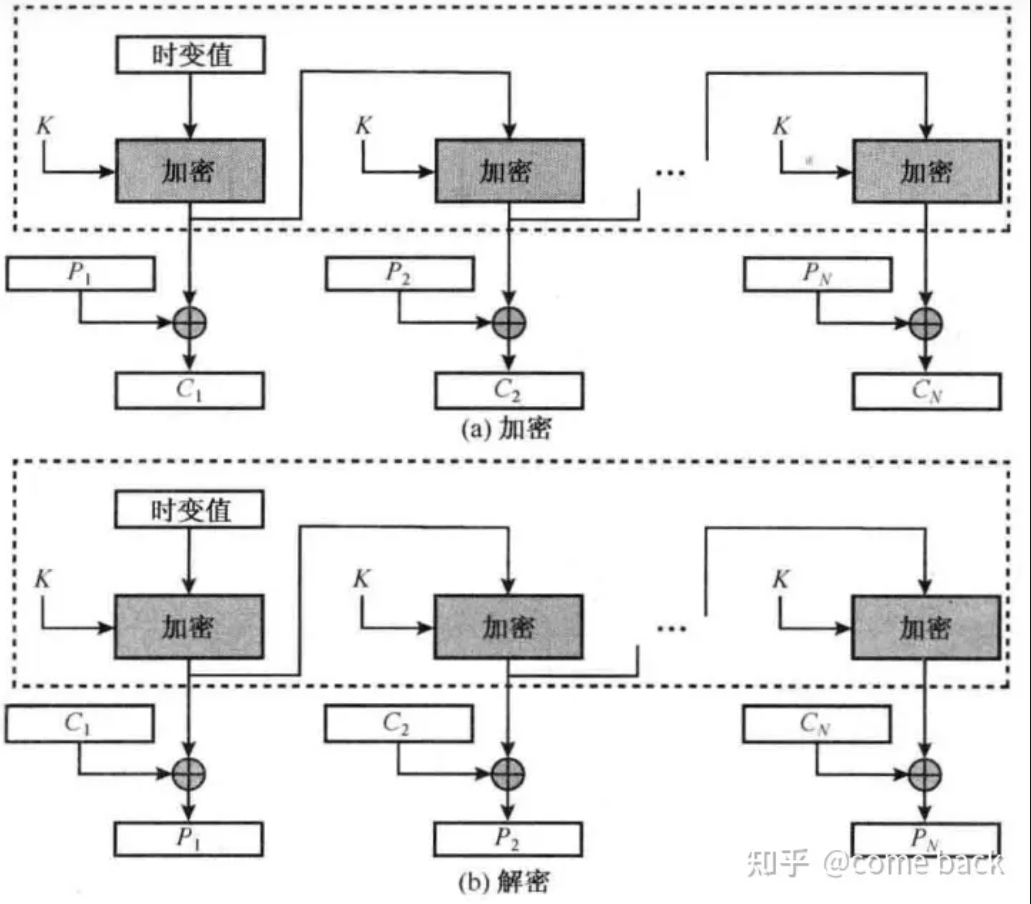
1.可以并行加解密,密钥流提前计算
2.与前面CFB相同,只计算密钥流进行异或
3.无错误扩散
4.抗算改不如CFB5.CTR 计数器模式 -> AES
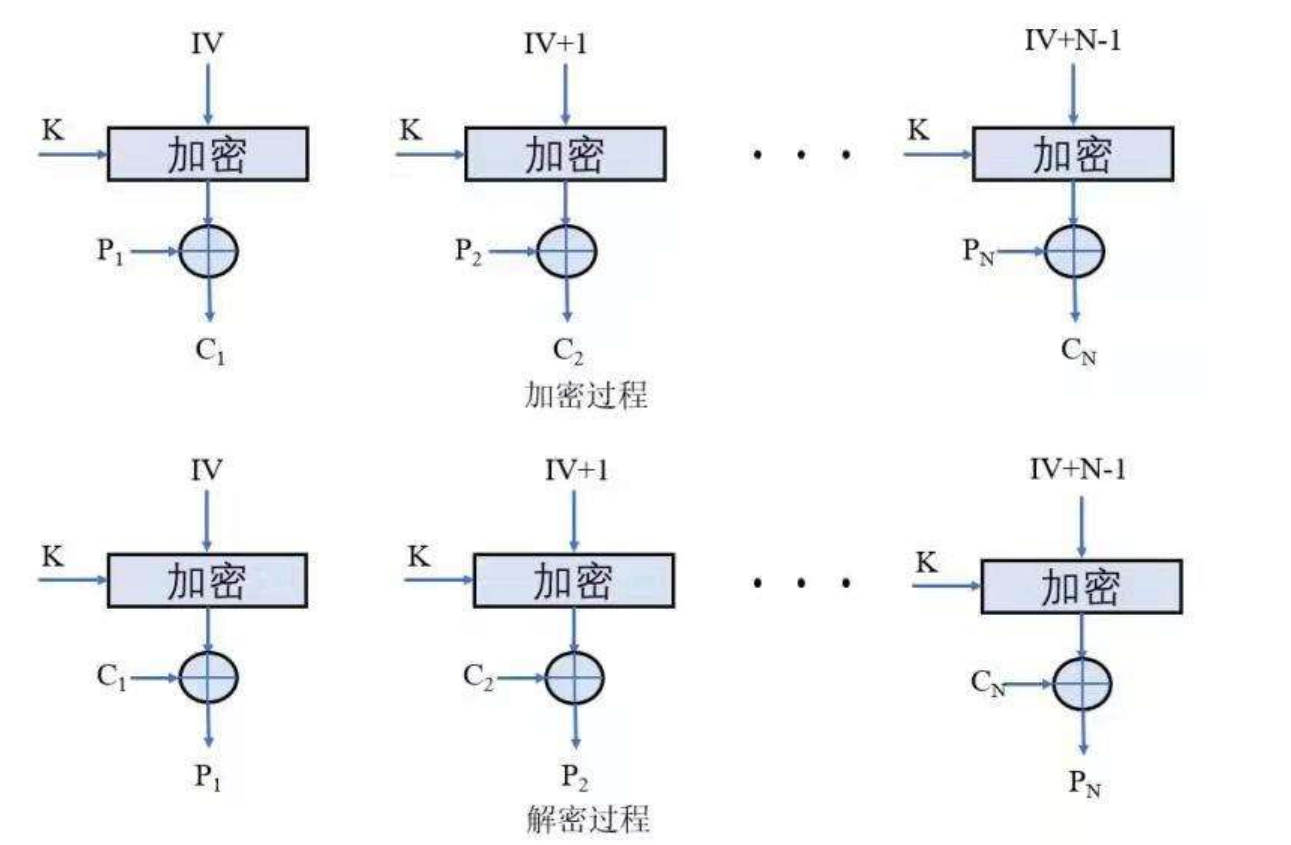
消息作为比特流进行加密,无须分组填充;
1.加密和解密过程只调用'加密算法';
2.存在'密文扩展'(IV传输的扩展);
3.密文块'分别独立'解密,无顺序要求(并行计算);
4.不存在错误传播;
5.适合'大于一个分组长度的长'数据加密.
(偷偷借用一下logiris大爹的总结图)
PRG和流密码
同步流密码
内部记忆元件的状态σi独立于明文字符的叫做同步流密码,否则叫做自同步流密码。
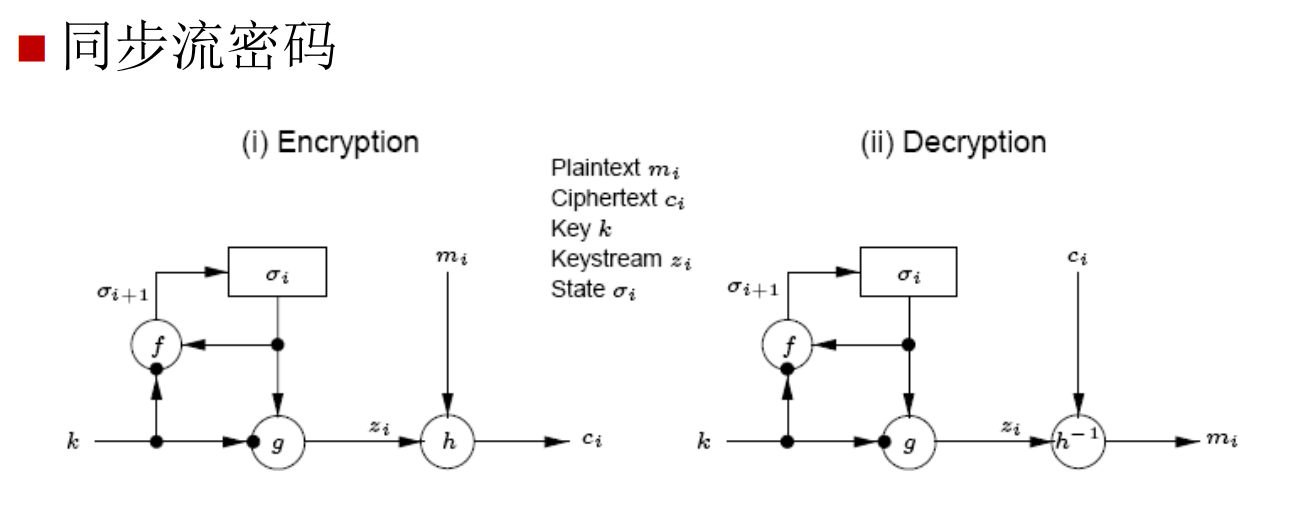
自同步流密码
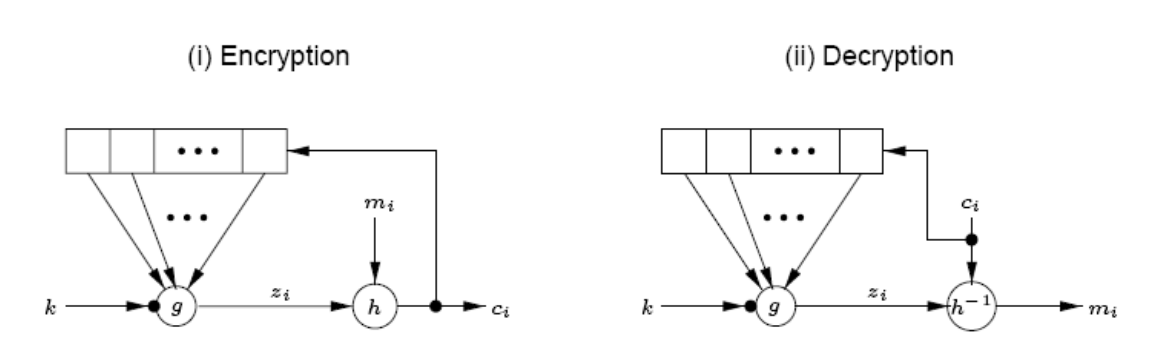
优秀流密码:
1. 极大的周期
2. 良好的统计特性
3. 抗线性分析PRG伪随机生成器
LFSR线性反馈移位寄存器
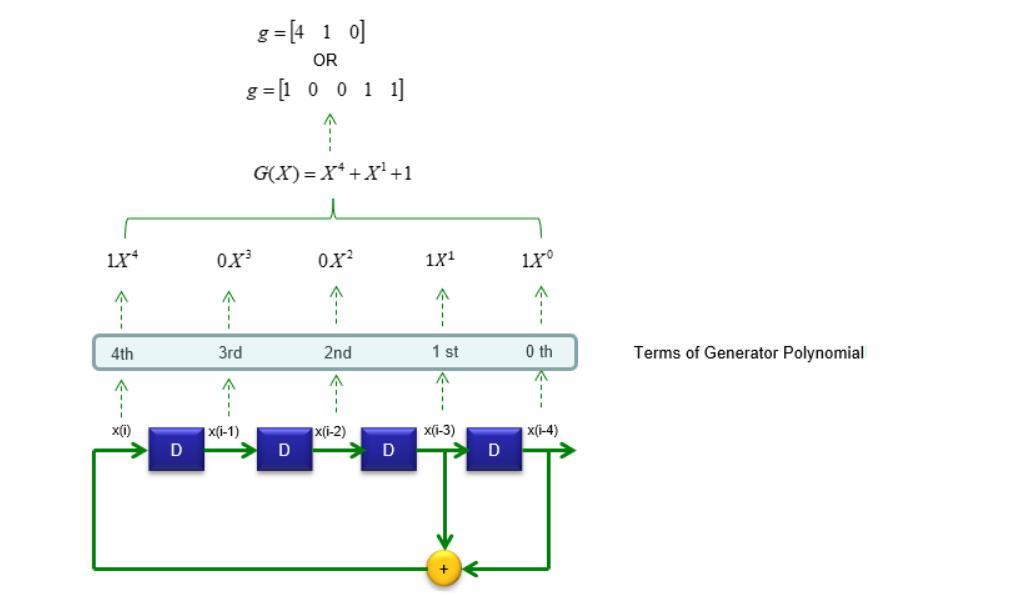
1. 每次计算进行一次移位,右边被移出的为输出,左边经过反馈函数计算得到新的值
2. 其中反馈函数可以由反馈系数决定
3. 每个反馈系数有周期,状态,输出,其中周期可以用(x^n -1)被整除计算特征多项式
这种递推关系可用一个一元高次多项式
m序列
m序列是一种特殊的LFSR
本原多项式
能够产生小序列的充要条件是其特征多项式必须为本原多项式(primitive polynomial )
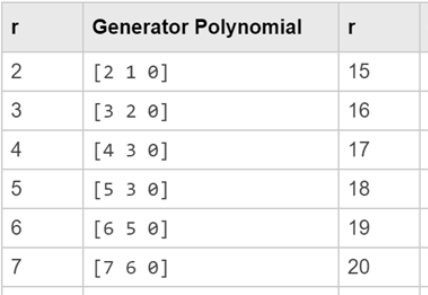
例如: 
m序列的安全性
已知一段序列,如果知道其反馈多项式,就可以将其后的序列依次 求出
已知序列能否获得相应的反馈多项式(或线性递推式)呢?
!!!
线性反馈移位寄存器综合解——Berlekamp-Massey算法 BM 算法
BM 算法待补
Rabbit
Salsa20
哈希与MAC
Hash函数
1. '功能' -> 保证数据'完整性'
电子签名等认证方案的关键技术,DSS、RSA数字签名
2. 将任意长度的消息x压缩为固定长度的值y
3. 应用
检测消息完整性
提高数字签名的速度
4. 压缩性
5. 有效性安全属性
'抗原像(单向性)'
'抗第二原像'
'抗碰撞'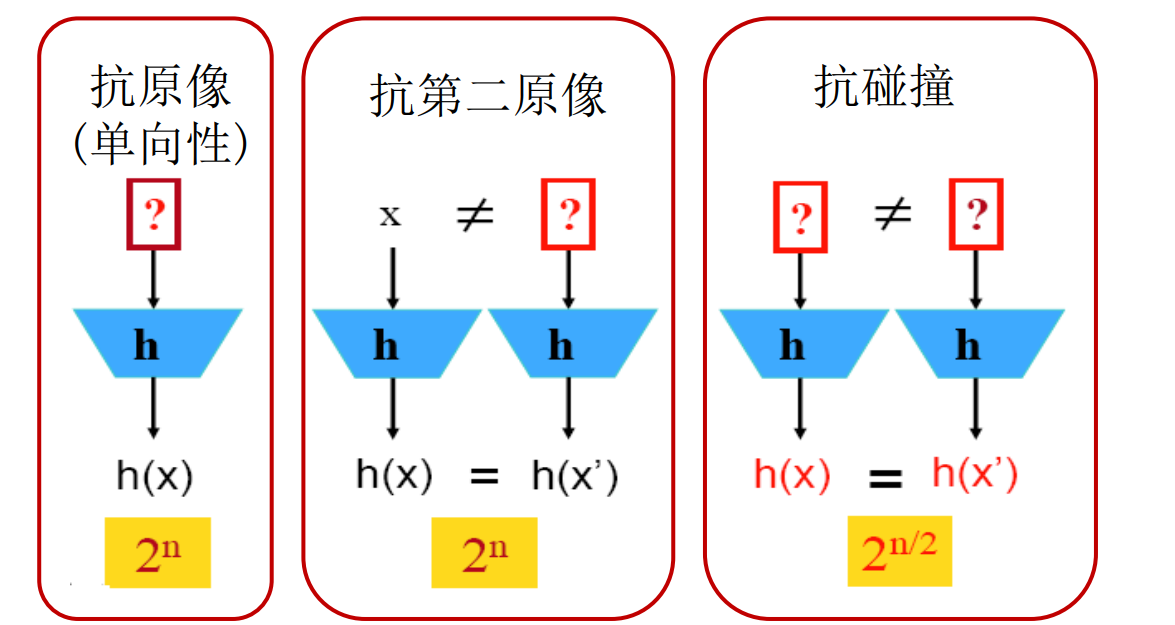
生日攻击

消息鉴别码
HMAC
HMAC的MAC算法是hash算法,它可以是MD5, SHA-1或者 SHA-256,他们分别被称为HMAC-MD5,HMAC-SHA1, HMAC-SHA256。
H是一个Hash函数
➢ K表示密钥
➢ B表示计算消息摘要时消息分块的字节长度(对MD5和SHA1是512比特,64字节)
➢ L表示消息摘要按字节计算的长度(对MD5是16字节)
➢ ipad表示0x36重复B次,opad表示0x5c重复B次。
➢ K可以有不超过B字节的任意长度,但一般建议K的长度不
小于L。当使用长度大于B的密钥时,先用H对密钥进行杂
凑,然后用得出的L字节作为HMAC的真正密钥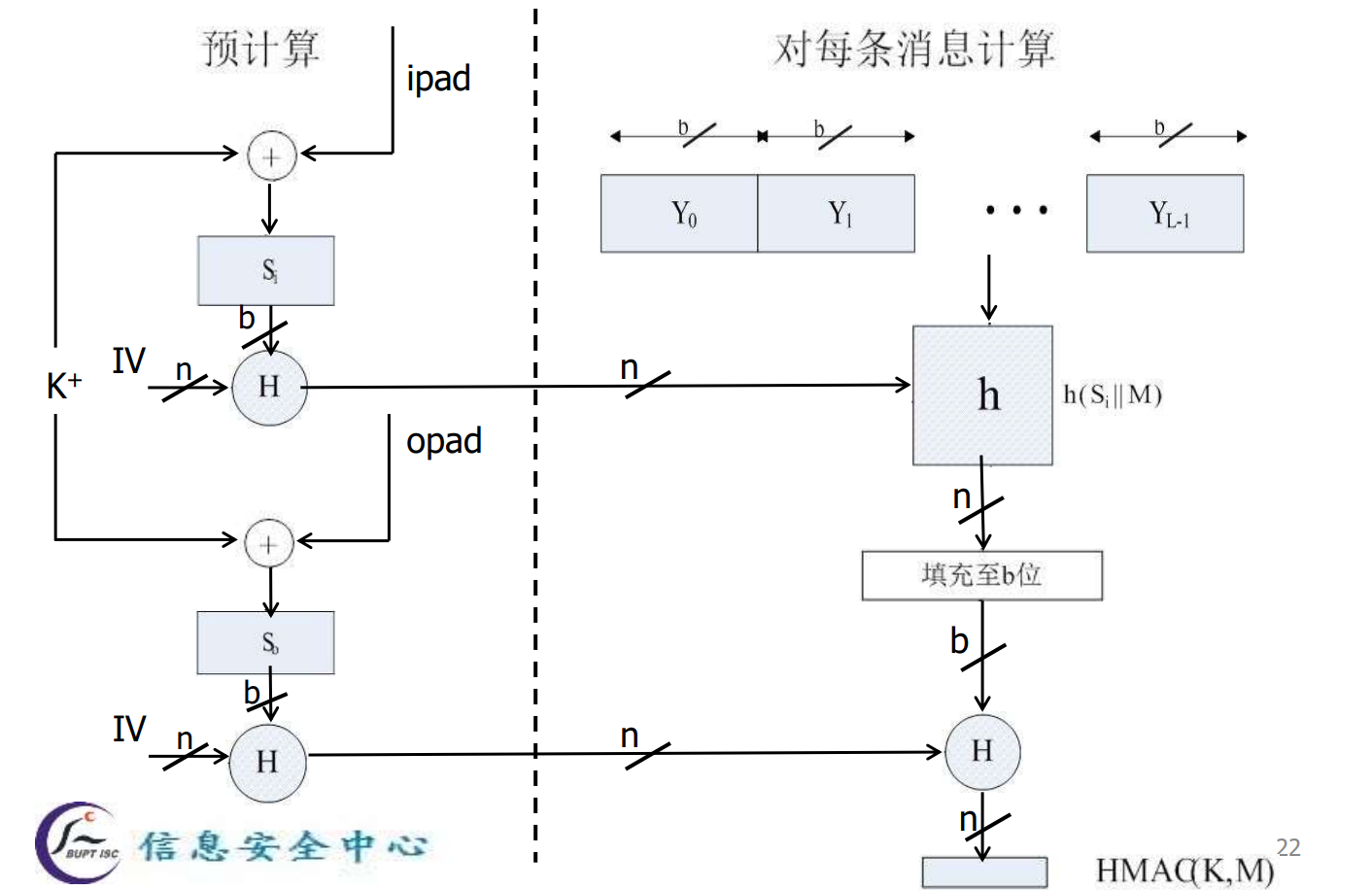
基于分组密码
CBC-MAC

数据不是加密算法分组长度的整数倍,则需进行消息 填充,填充方法有
首先对需要计算MAC的数据的右边填充若干个或零个 “0”比特,以便得到一个比特长度是n的整数倍的数据串;其 次,在所得到的数据串的左边 填充一个n比特组,该组包含了 未进行填充的数据的比特长度的二元表示,其左边用“0”补齐
ECBC-MAC
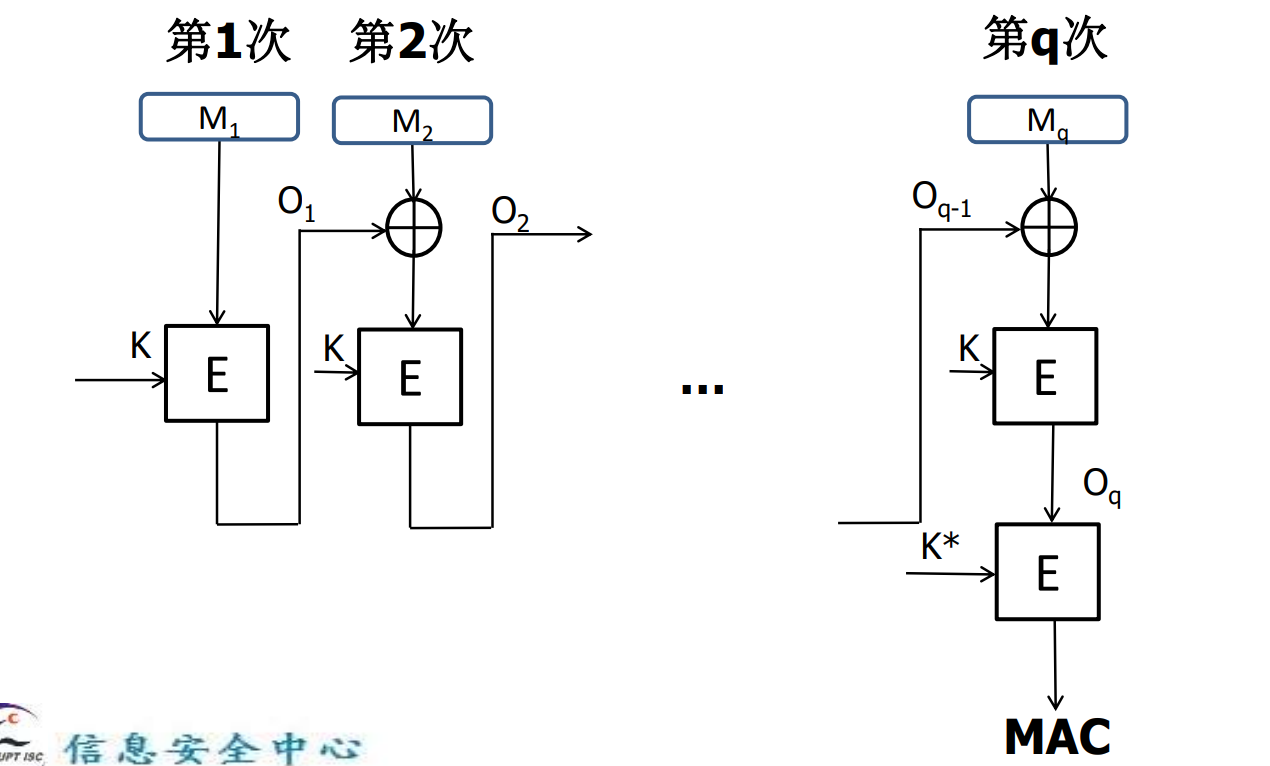
公钥密码学
模型
密钥生成过程
加密过程
解密过程
背包问题的OTF






RSA



RSA函数及其应用
密钥长度介于1024比特至2048比特之间的RSA是安全的
ElGamal单向陷门函数



椭圆曲线单向陷门函数
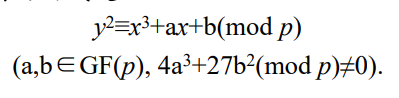
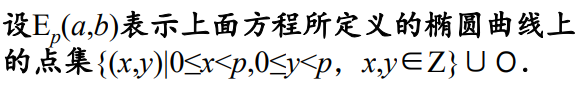




数字签名
RSA



DSA

椭圆曲线


